Finite Element Analysis of a Rope Wound Around a Capstan Drum

You don't need to be a pirate or sale the high seas to enjoy the analysis of a rope wound around a Capstan drum, although it probably doesn't hurt either.

Capstan

When a flexible tensile member such as rope, belt or chain is wrapped around a drum the tension in this flexible tensile member creates a normal force that is perpendicular to the surface of the drum. This normal force coupled with the friction that exists between the flexible tensile member and the surface of the drum will reduce the tension in the flexible member.

This may seem a little strange to non-sea faring folks and non-pirates so let's look the equations themselves and a simple example problem to see how they can be practically applied.

Capstan Equation

Let start with a simple example, then we will move on to something more complex.

Here we have a Blue Drum and a Green Rope. One end of the Green Rope is firmly fixed to the side of the Drum and a load is applied to the other end of the rope tangential to the drum.

Simple Drum Example

If the coefficient of friction between the Rope and surface of the Drum is 0.2 how much tension is in the rope where it attaches to the Drum if we apply a load of 1000 lbf to the other end?

Now if there were no friction this would be simple. 1000 lbf applied to the rope at one end would mean that we need 1000 lbf at the other end applied in the opposite direction to prevent the free body motion of the rope.

However with friction included, the tension the rope decreases along the circumference of the Drum. Lucky the Constan Equation is very easy to implement in the simple example.

Simple Example Solution

Now that we have a better understanding of the Constan equations and it's practical application, let's see if we can solve a slightly more complex example using the the Finite Element Method, as this is a non-linear problem that includes contact we will need to use ANSYS Mechanical for our Finite Element Analysis Software.

For this example we will use a 1.0 inch Drum and a 0.1 inch Diameter Rope that is wrapped 2 times around the Drum. The Coefficient of friction between the Rope and Drum will be set to 0.15.

Example 2 Rope wrapped 2 times around a Drum

To simplify the FE-modeling process the Drum was modeled as Midsurface so that is may be meshed with shell elements and the rope was modeled as a line body. If anyone would like this CAD model please contact me and I will send it your way. The Geometry model was meshed with a default Element Size of 0.05 inches.

Default Mesh Size 0.05 inches

The Rope Model Type was set to "Cable" and the Cross-Section of the Rope was defined to have a Radius of 0.05 inches.

Model Type set to Cable

The Rope has a Circular Cross Section with a Radius of 0.05 inches

A Contact will be created between the Line that represents the Rope and the Mid-Surface that represents the Drum.

Frictional Contact, Coefficient of Friction = 0.15

As the Rope is modeled as a Line Body and the Drum is modeled as a Surface Body, the Pinball Radius for this contact needs to be sufficiently large to capture the interaction between these different bodies. For this geometer the Pinball Radius was set to be 0.1 inches. The Interface Treatment was set to be Adjust to Touch to eliminate any gaps that may exist within the modeled geometery.

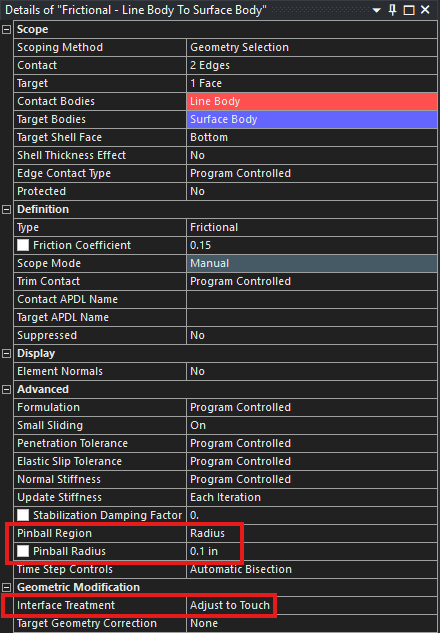
To attach the end of the Rope to the Drum will use a Bonded Contact. For this contact we will send the Pinball Radius to 0.1inches.

Ok my sea fairing crew lets apply some Constrains.

We aren't concerned with the Drum or the forces applied to the Drum so we will simply be fixed. This may not always be the case so proceed cautiously when fixing large portions of you model.

We can now apply a 400 lbf force to the end of the Rope. This Force is applied co-linearly to the line the represents the Rope.

Any good sea fairing crew knows they must plan ahead, as the ocean can be an unforgiving place. As this is a non-linear model that utilizes Cable Elements, we must change turn Large Deflection on in the Analysis Settings. We should also used Step Control to verify that our loads are applied slowly and aid in convergence.

Let solve this Non-linear model and see if we can identify some useful results. This relatively FE-model solves in under 17 seconds, despite the Non-linear contact and Large Deflection.

When we look at the contour plot of the Axial Tension in the Rope we see how the Friction between the Drum and Rope reduce the Axial Tenison in the Rope.

Axial Tension in Rope

Before we believe these results let us evaluate this second example using the Capstan Equation.

Example 2 Capstan Calculations Hold Force = 60.73 lbf

The Hold Force identified using ANSYS Mechanical was found to be 60.81 lbf, the Hold Force identified using the Capstan Equation was 60.73, resulting in an Error of less than 0.125%. This is represents an excellent correlation between a Finite Element Model and Capstan Equation.

Thank you for taking the time to read this article and please contact me if you have ideas for future articles.

John Parsons

Analyst

MESim LLC

John.Parsons@MESim.us

www.MESim.us